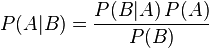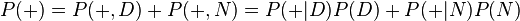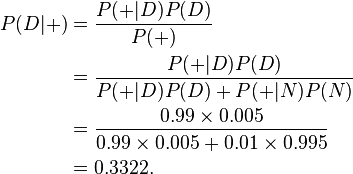很久的时间没有更新了,一是因为每天加班到比较晚的时间,另外,公司不能上网,回家后就又懒得整理,最近在看机器学习实战的书籍,因此才又决定重新拾起原先的博客!
今天讲的是第三章的贝叶斯分类方法,我们从一个简简单单的例子开始入手:首先看(1)图中的例子,假设有一个装了7块时候的罐子,其中3块时黑色的,4块时白色的,从中随机取出一个石头,那么这个石头是灰色的概率是多大?


(1) (2)
我们可以很轻易的计算出取出一个灰色球的概率是4/7,取出一个黑色球的概率是3/7,但是假如这些球被放在两个不同的罐子中,如图(2) :A中有3个黑球,2个灰球,B中有三个灰球,两个黑球。那我们从中取出一个灰球的概率是多大?我们很自然的联想到要首先知道是从A中去取还是从B中去取。
假设从A中取得概率为Pa,从B中取得概率为Pb,那么我们取出一个灰色球的概率为:
Pgray = ( 0.4 ) * Pa + ( 0.6 )* Pb
此时的0.4 和0.6 分别表示为从A和B桶中取出一个灰色球的概率,我们也称其为条件概率, 记为P(gray | A) = 0.4,P(gray|B) = 0.6
我们引出维基百科上关于贝叶斯公式的定义:
贝叶斯定理是关于随机事件A和B的(或)的一则定理。
其中P(A|B)是在B发生的情况下A发生的可能性。贝叶斯定理中,每个名词都有约定俗成的名称:
-
P(A)是A的或。之所以称为"先验"是因为它不考虑任何B方面的因素。
-
P(A|B)是已知B发生后A的,也由于得自B的取值而被称作A的。
-
P(B|A)是已知A发生后B的,也由于得自A的取值而被称作B的。
-
P(B)是B的或,也作(normalized constant).
按这些术语,Bayes定理可表述为:
后验概率 = (相似度*先验概率)/标准化常量
也就是说,后验概率与先验概率和相似度的乘积成正比。
另外,比例P(B|A)/P(B)也有时被称作标准相似度(standardised likelihood),Bayes定理可表述为:
后验概率 = 标准相似度*先验概率
[例一(维基百科)]
贝叶斯定理在检测吸毒者时很有用。假设一个常规的检测结果的敏感度与可靠度均为99%,也就是说,当被检者吸毒时,每次检测呈阳性(+)的概率为99%。而被检者不吸毒时,每次检测呈阴性(-)的概率为99%。从检测结果的概率来看,检测结果是比较准确的,但是贝叶斯定理却可以揭示一个潜在的问题。假设某公司将对其全体雇员进行一次鸦片吸食情况的检测,已知0.5%的雇员吸毒。我们想知道,每位医学检测呈阳性的雇员吸毒的概率有多高?令“D”为雇员吸毒事件,“N”为雇员不吸毒事件,“+”为检测呈阳性事件。可得
- P(D)代表雇员吸毒的概率,不考虑其他情况,该值为0.005。因为公司的预先统计表明该公司的雇员中有0.5%的人吸食毒品,所以这个值就是D的。
- P(N)代表雇员不吸毒的概率,显然,该值为0.995,也就是1-P(D)。
- P(+|D)代表吸毒者阳性检出率,这是一个,由于阳性检测准确性是99%,因此该值为0.99。
- P(+|N)代表不吸毒者阳性检出率,也就是出错检测的概率,该值为0.01,因为对于不吸毒者,其检测为阴性的概率为99%,因此,其被误检测成阳性的概率为1-99%。
- P(+)代表不考虑其他因素的影响的阳性检出率。该值为0.0149或者1.49%。我们可以通过全概率公式计算得到:此概率 = 吸毒者阳性检出率(0.5% x 99% = 0.495%)+ 不吸毒者阳性检出率(99.5% x 1% = 0.995%)。P(+)=0.0149是检测呈阳性的。用数学公式描述为:
根据上述描述,我们可以计算某人检测呈阳性时确实吸毒的条件概率P(D|+):
尽管我们的检测结果可靠性很高,但是只能得出如下结论:如果某人检测呈阳性,那么此人是吸毒的概率只有大约33%,也就是说此人不吸毒的可能性比较大。我们测试的条件(本例中指D,雇员吸毒)越难发生,发生误判的可能性越大。(这个相信能给曾经去体检结果非常不好的人一个乐观的消息)
[例二 (Machine Learn in Action)]
机器学习的一个非常重要的作用就是对文本进行分类,我们使用Python进行文本的分类
(未完待续)
参考:[1]刘未鹏
[2] Machine Learn in Action, Peter Harrington